Creating a Mathematical Theory of Software
In this series, we'll explore how mathematical and software abstractions are connected and why they matter, including how the bundle of rules, axioms and proofs pop up in surprising areas
Instead of being another category theory article or advertisement for a new software paradigm, we’ll look at things from a different perspective without losing out on the details, building up our understanding of the motivations and working mechanisms of “dry” mathematical concepts relevant to creative software.
If you’ve ever had fun tinkering with programming puzzles and games yet dislike math in educational settings, there might be a good reason, and you’re not alone. Despite that, you might’ve been doing mathematics without wielding the full power of its toolkit.
Mathematics isn’t what you think it is
Imagine you are conversing about mathematics with a random person off the street. In that case, it seems that mathematics is a laborious, number-crunching, creatively shallow field practiced by a minority of numerically-inclined outcasts. Among software engineers, broadly, mathematics is seen as a collection of equations and methods useful for solving practical problems.
When mathematics is treated as a cookbook, it becomes hard to argue that it’s a web of ideas about how to make such references and magic spells in the first place. Possessing such knowledge would be helpful in anything related to the creation of methodologies, thought frameworks, and other systems where the relations and functionalities embody the substrative gear meshing.
The everyday view of mathematics as a manual of tailored solutions to concrete problems creates the misconception that, if research mathematics were an extension of endless arithmetic drills in schools or engineering classes, its pursuit is a waste of time in the age of computerization. The other side of the coin — mathematical proofs — remain hurdles to get past, formalities in textbooks of no use.
It seems unintuitive to argue how software is a type of mathematics. Yet software isn’t mathematical because it utilizes concoctions of formulae from trigonometry or calculus for visual effects and virtual worlds. It’s mathematical because it concerns itself with logical relationships between abstract mathematical objects. Even more surprisingly, whole programs, programming languages, and more can be treated purely “mathematically.”
At this point, it could be argued how a specific description of what mathematics is really about will help with optimization, and that’s the be-all, end-all of all software problems. If mathematics is all about logic, or something along those lines, all of your issues will be fixed with a couple of simple changes. Management is no longer breathing down your neck; you can finally take that vacation without pushing to production on a Friday.
Unfortunately, that’s too naive and not the reality of neither programming nor typical mathematical practice. The fundamental difference in the perception of mathematics and the artificial divide between software engineering and mathematics is harmful to mental models of software, shepherding our decisions surrounding software architecture, framework choices, and way more besides optimization via logical streamlining.
That’s where mathematical practice comes in, the art of creating new logical frameworks and even abstract computational models. Some areas of software engineering are familiar with the process we’re going to explore, but the failure to recognize it as mathematical tears it apart from taking it further — concernedly in terms of practical matters, not abstract mathematical simplicity or beauty.
Likewise, mathematicians benefit from “digitizing” theoretical mathematics¹. Later, we’ll see how mathematical practice is dialogical. The mathematician is as much of a participant in the process of doing mathematics as mathematics is an agent guiding the answers, just like the conversation between a programmer and a computer.
Approaching software as a mathematical theory shifts focus from mechanized design to emergence
Let’s explore the relationship between mathematical practice and software from the outskirts by creating a program about something uncharted.
Suppose we’re in a new city and would like to find the shortest path to our hotel from the airport by foot (since we’re adventurous), and this has never been solved before by Dijkstra. What’s worse, graphs don’t exist.
There are many things to consider — all the different routes from any point on the map, their combinations, and then, well, what makes one path better than another? Would we have to distinguish between turns, and how do we codify this information? The number of questions keeps growing at every step. How do we model this in the first place?
The obvious choice is to limit information. Strip away the landmarks, the features of the city, the bakeries you’d like to visit on the road, and focus on the substance. We decide to envision turns on the map as points and the roads connecting them as lines.
Our abstract model of the map becomes a game. Imagine walking along those lines, reaching the points, and deciding which path to take next. Is it possible to skip some of the points? Could we add more lines that represent the sum of a couple of them? What are the rules for moving around our web? We can create them and see what happens.
As we experiment with our primordial graph, we begin creating notions of graph theory while working on comparing paths and how to calculate them in the best way, taking the least amount of work. Simultaneously, we’re creating a theoretical framework for modeling similar phenomena and procedures for working with them.
Our new model of so-called graphs will be immediately helpful for illustrating connections and relationships between objects. In this case, our “objects” are turns on a map, and the relationships between them are actual roads.


Since we’ve familiarized ourselves with generalizing a problem into a graph, we can make connections between them and other problems besides finding the shortest paths on a map, even if they seem outlandish. It’s similar to other kinds of knowledge, since our perception of the world depends on our notions about it.
🪄 However, creating a mathematical theory adds
the process of verification (whether a point is a turn on the map),
methodologies for turning one thing into another (whenever you encounter a turn, treat it as a point),
rules (a point can be reached only if it’s connected with lines in a specific way),
and operations (walking/traversal), among other things.
Together, they create something akin to a computer program, a system of interlinked relationships. The rules and game pieces — the mathematical objects — are mannequins, taking on the abilities and appearances limited by the imagination of the mathematician or programmer alone.
Once the game is set, the software structure — the choices of data structures, algorithms, control sequences, memory management, and systems design — sprouts from the groundwork.
For various reasons, that’s not typically how we present mathematics. The utility of the familiar often beats the need, and demand, for complete innovation. Only this might’ve been truer at a time when we barely dreamed about a multitude of new language models, programming languages, and image recognition techniques.
Creativity stagnates as it relies on cherry-picked rules passed down by mathematicians to software engineers long ago
Innovation is the new currency. The ever-increasing complexity of software such as AI requires the invention of new theories and procedures, much like how we imagined inventing our version of graph theory or applying existing mathematics that collects dust in the confines of academia instead.
What’s the impulse behind innovative, out-of-the-box approaches that defy rules, establishing new ones from far-apart ideas, and connecting them into a robust system? Reactions between unconnected ideas generating new explanations might happen because of something called abductive reasoning — coined by the logician Charles Peirce.
If our software behaves strangely due to a bug, and we infer what it might be from the behavior, we’re deducing that the software bug caused the issue. Most everyday software development and engineering hinges on deduction alone (unless you’re a functional programmer, then you’re also using a lot of induction).
Abduction is different. Instead of following a clear path of reasoning from A to B, such as “The ground is wet only when it had rained. It’s raining, so the ground must be wet”, it pulls and evaluates the most fitting priors from a body of knowledge to infer the cause of the end result.
To understand this, imagine that we live in a glass dome, tasked with creating an artificial climate to terraform the environment. Suddenly, the glass is covered in droplets. What might’ve caused it? We access our internal knowledge network: the sprinklers aren’t functioning yet, there aren’t any plants on the surface that might’ve evaporated water… maybe there was a puddle? We conclude that the puddle evaporation was the most likely cause for the misty glass, and we’ve just engaged in abduction.
We had to take quite a few detours in our neural pathways to get to a conclusion using abduction, evaluating the likelihood of a process, instead of following a direct chain of events. The same happens whenever we have to create something new, be it a painting, a programming language, or an AI.
In the case of a painting, an artist might have an end result in mind and synthesizes different approaches to color, lighting, and perspective from their memories and built-up knowledge, evaluating the best ways to bring their idea to fruition. But when something as complex as an AI is concerned, we need to draw from a mixture of mathematical, logical, and philosophical bodies of knowledge.
That’s alarming when most people know how to follow rules — such as calculating the circumference of a circle or solving an equation — but not how to invent them, making them work together like a piece of machinery. After all, only mathematicians are prepared to glue theoretical ideas together into a cohesive system that runs like clockwork, generating the tools others will use.
Instead, we have to build up the knowledge and skills needed to create new lenses for examining the world in a formalized way, without limiting it to the widespread understanding of what is mathematics.
Does it mean that everything and anything is mathematics, be it the whole world of art, engineering, and the sciences? Not really.
It took at least hundreds of years of work to describe what it means to have a system of equations, arriving at its usage as a computer in its own right -- an algorithm for calculating values of unknown variables -- long before the silicon age. The minimalist computational machines of yore all shared one similarity: in order to make them work, they were described in a mathematical theory, a system we defined above (in our toy graph theory example) as having the ability to prove the properties of the objects of interest and having a specific set of rules and operations.
It's possible to argue that mathematical theories and not logic or skill underlie the cognitive processes of art-making, science, or engineering paradigms, even when they're not explicitly defined, as it's probably possible to define them in many instances. But software engineering is directly connected to the practice of inventing mathematical theories, which means that with sufficient understanding, software engineers can create new theoretical frameworks like mathematicians today instead of working in isolation from each other.
Why are new mathematical theories necessary at all, and what does it really mean for software? In order to solve problems associated with ever-increasing complexity in modern computation, we must re-evaluate our approaches and tailor them to new paradigms. Whether you're against it or not, something like AGI shouldn't and probably cannot be created through brute force or stacking existing ML frameworks together.
The beginning stages of AGI will likely involve the creation of a mathematical theory for intelligence -- the framework with rules and operations and a proof system to verify properties, processes, and conclusions for various forms of intelligence. Then AGI could be represented as various mathematical models arising from the theory.
Overall, we’re facing the question of conceptualization of novel abstractions — encompassing a unique way of the generation of knowledge in the first place, new data types, and more — leaving the software as an implementation detail instead of treating it as a guiding light.
The focus shifts from being constrained by the implementation to having an atmosphere of theories, easing the movement between prototype models of the same concepts. However, it doesn’t mean that implementation is easier or less important than conceptualization. It might take many painstaking years, maybe even centuries of progress. Necessarily, new advances in the practical realm of implementation change the fashion in theoretical works, so it must be a collaborative effort.
Most programmers have little choice when it comes to algorithms, data structures, types, or even software design, using the classical results picked for them in existing programming languages or textbooks. At the same time, mathematicians develop new concepts, sometimes giving the reason for making programming easier.
The news never reaches the craft for experimentation and feedback, and those who have to design new approaches rarely interact with mathematicians for inspiration. Game developers and many others often work out new mathematical theories without realizing it, but merging with mathematical practice might bring new ideas to fruition or help the implementation.
Before embarking on an academic journey into pure (abstract, proof-based) mathematics, I was impatient to turn anything I worked with — be it physics, embedded systems, or game engines — into an invention because I couldn’t help myself digging deeper into the fundamentals and experimenting with tweaking or breaking them. At the time, I believed mathematics is all about routine drills and memorization and didn’t know my process was inherently mathematical until I started working on creative software, such as games.
I began working on Idu, a sandbox-style simulation game about strategizing around the growth and upkeep of procedural plants with a mind on their own. To my surprise, obscure video game development and pure mathematics turned out to be incredibly alike, following in the footsteps of the invention of the toy graph theory or the fantasy of how one would work on something like AGI.
We had to create a specialized 3D game engine and a novel way of generating and interacting with continuously unique plants that calculate whether and where they should grow new branches according to photosynthesis, soil moisture, and more.
Instead of looking up specific equations, a typical day would consist of playful experimentation on paper and combing through research articles in different fields to help with intuition for our theoretical framework, which didn’t exist. We had to have the courage to break the rules, integrating several theories into a single entity embodying artificial life.
Game programming isn’t unique, though. Instead, this characterizes groups of people, often self-taught or disillusioned by linear progression in education, seeking a different outlet, motivated by curiosity and play for its own sake. They’re situated amongst modern creators of the digital Renaissance, congregating in online communities to learn how to synthesize patches of disorganized knowledge into computer games, esoteric programming languages, musical instruments, etc.
At one point, they’re engaging in discussions on the notion of equivalence and the nature of mathematical objects, all without consciously realizing it’s mathematics. Eventually, they get stuck in knots of logical roadblocks, such as how to implement this or that type or verify the correctness of something. Yet the recipes for untangling lie in the fields at the intersection of abstract mathematics and the foundations of mathematics — the thread weaving domain-spanning networks together.
In that world, mathematical objects are contextual. Forget about numbers, sets, and functions between them, and familiar geometric figures underlying the typical flavor of mathematics. The associations and webs intertwining placeholder objects take center stage, with their properties arising from the patchwork. The work of a mathematician is similar to that of a game designer, then, and the software engineers participate in the games with rules laid out to them.
If you want to make the rules, then a mathematician’s intuition is the missing piece of the puzzle.
Software paradigms are lacking, but inventing new ones misses the mark
When mathematicians conjure ideas about the behavior of different structures, fundamentally, it’s a process of creating new logical universes, spanning all possibilities with the constellations within. Broadly, when a general theory is true for all instances of something, the application for a specific case can be extracted from it; but proving the validity of a theory based on a particular object wouldn’t work.
The process is backward compared to software design at large, where it’s tailored to the problem, and a software theory for the general solutions of all problems of this type wouldn’t be reasonable. Instead, the software can be a specific instance of a mathematical theory, like a different operating system running on the same hardware.
A few detours from the concrete to the inspirational will give us a clue about how conceptualizing software in terms of a mathematical theory changes our approaches.
The first stop on the way reveals how software is multi-dimensional, and mathematicians are ready to prove it. A dimension may not be the familiar, spatial kind but a notion for concurrency. We could say that software with four parallel processes is four-dimensional, analyzing its structure in some four-dimensional mathematical theory. Like spatial dimensions (in a three-dimensional space, we may have points on both the x, y, and z-axes simultaneously), we have multiple software processes occurring at the same time.
One way to analyze or even create software would be to view the “skeleton” of associations in the program. The resulting structure could be visualized as a graph where the connections are malleable, replacing several pathways with one via composition. Think of it as the ability to put letters side-by-side, resulting in words.
After defining the concatenation of letters as a+b=ab, we can also prove that having the ab in abracadabra is equivalent. Let’s say that our system only has one object, a meaningless placeholder “*”. And the letters between the copies of the same object are arrows, creating a word when they’re put together.

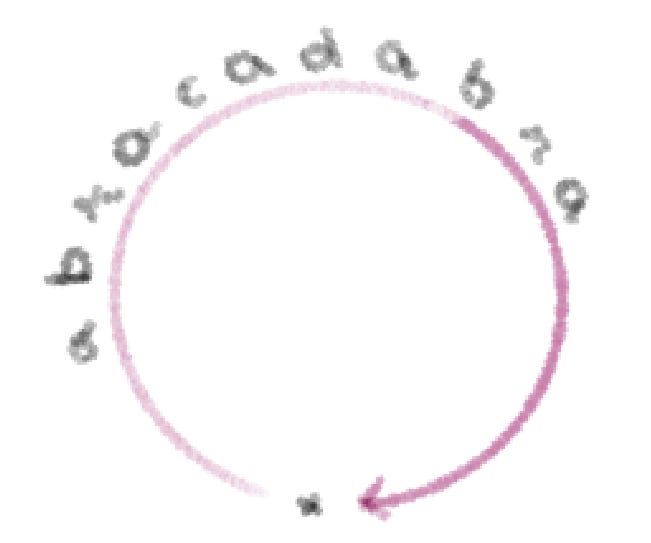
The letters are stand-ins. They could be anything from functions to data structures in a program; we’ve just given them convenient labels to combine software processes together through their associations, creating the interconnected skeleton of a program.
If anything can be labeled as those letters, then what about the logical circuitry of a processor? Dense logical circuits and languages could be compared similarly — even between each other, with their logical infrastructure becoming labeled as the “letters.” A mathematician might be tempted to find a uniform way to convert electrical schematics packed with boxes and wires into an alternative format, like a sequence of digits.
Finally, it might be even more unexpected that software can be translated into something as different as a geometric image, such as a Klein bottle, keeping the correspondence between all of their interlinked relationships in the form of “surfaces” and “sides,” perhaps. If we could use arrows to replace functions or data, why not imagine the resulting sequence of relations in terms of shapes?

These magical-seeming transformations allow us to use various mathematical theories to inquire about the same object in varying forms, like chemistry. Water is “drinkable” in its liquid form; software is “round” in its geometric form. We could use topology (broadly, a study of spaces not necessarily equipped with distances) to study software in this state of matter.
As a result, it becomes possible to find a variety of simpler but equivalent systems in a formal, mathematical way.
When we fooled around with the invention of graph theory, we devised a method of distinguishing between turns and roads on a map by associating them with points and lines, respectively. It equipped us with the ability to take a look and say, “these streets can not be “points” in our theory because they’re intersecting, which means they’re “lines” and the intersections are “points” instead.”
On the surface, it might seem too obvious, although we’ve just proven a fundamental property of our model of an urban map. So if we turn software into a funky geometric figure, our theory's bundle of logical tools will help similarly determine related functions, data structures, and processes.
Perhaps this sounds similar to object-oriented programming (OOP). After all, we’re dealing with abstract objects that could represent anything, and we’re trying to find associations between and procedures for combining them.
Although mathematical abstractions are often compared to software abstractions at the level of OOP, they differ greatly in their purpose and approaches. Designing classes with virtual methods that several other classes could inherit doesn’t provide the tools for ensuring our designs aren’t complicating the software logic or creating redundancies.
Software paradigms by themselves, such as OOP, data-oriented design, etc, are the cowboyism of generalization processes lacking the provability and robustness that mathematics provides. That’s fine because they’re not designed for it.
They’re structural, not analytic tools, so considering them equivalent feeds the wrongful impression that picking one software paradigm over another is correct in a mathematical sense.
Mathematical abstraction and structural software abstractions are complementary, not replacements of one another, and the “correctness” of software paradigms can only be judged in the realm of engineering — whether the model of data and processes fits the problem it tries to solve.
The logical associations lie beneath the resulting classes and methods, given that our choice is OOP, and overlay the resulting program at the same time. A mathematical theory would say that the way we define our data, like whether something is a list or a hashmap, also dictates the operations we can use on them and their efficacy.
In that sense, we’re only used to dealing with mathematical formalism on the level of programming language or algorithm design at most, even though whole programs can be viewed from the same lens.
Agnostic to the paradigms, treating software as mathematics could guide us towards better choices of data structures, correct our algorithms, and make sure the whole program is verifiably correct.
We’re used to abandoning intuition in favor of template solutions, including heedlessly running toward category theory
So in the beginning, we turned an urban map into a lifeless composition of dots and lines, representing all of its buzzing and difficult choices of turns and sidewalks in that structure.
The translation of structures in software, numbers, and familiar urban maps into generalized mathematical objects keeping the associations between them, is one of the motivations behind the application of category theory (with bonus ingredients, like compositionality).
Yet comparing category-theoretic concepts directly to structures in programming without rolling up our sleeves to perform the procedures or the verification of our hypotheses serves no purpose.
Functional programmers may be comfortable with juggling monads and endofunctors, but obfuscation is more likely than simplification as intended by category theorists. Unsurprisingly, how can one navigate mathematical practice if they don’t recognize their craft as a part of it?
Category theory is often in the spotlight as it is related to abstractions in functional programming. Still, the comparisons often pay attention to the notation or words used in the theory instead of its mechanisms, much like how new programming paradigms without any additional mathematical formalisms are proclaimed to support more logically correct programs.
Besides, category theory is one of many metatheories of mathematics, a river etching out the cartography of mathematical foundations, shouldering type theory, logic, and others, forming an ecosystem of generative, systematized inquiry.
The difference in various theories in mathematical foundations is similar to the difference between languages. The interpretation of the objects, their associations, and their “translations” into other theories depend on said language, with its advantages and limitations.
However, conventional languages limit the placement and relationships between words in sentences. Translating from one language to another replaces this information with the target language’s rules, dissolving some meaning of the words, whereas mathematical processes preserve them.
Jumping between mathematical languages without losing the meaning or structure of the objects matters little by itself. Were that the only perk, we’d converge to the most straightforward language and wouldn’t have mathematics.
Mathematics is characterized by its diversity of disciplines, whereas the line between them is blurred and mostly sociological — remember looking at different facets of the same object. The ability to translate between their core fabrics enriches our view with new ways of interfacing with the mathematics.
What happens if we translate the entire collection of the objects of study in an array (also known as an ordered set in mathematics or a list in computer science) — and the ordering between them — into a graph-like structure with additional rules of play?
Sometimes we’ll see lone dots in this new galaxy — connected to others but only in one direction. We zoomed out of the mathematical discipline to look at its structure in full context and perhaps discovered something about our “dot” that we could never see before.
The initial discipline didn’t define “an object which hovers over others in the graph.” We know it’s equivalent to saying, “being on top in the graph signifies the largest element in the array.” What happens if we flip the graph so that the uppermost element is on the bottom? We reversed the array!
Now we have a method for expressing the uniqueness of said “dot” and its connections to others, returning to our discipline with newfound insights. It wasn’t that interesting with a single array, though.
Considering every possible array out there as an object (not what’s “inside” them) through “special arrays” (like bottom or top elements in the previous example) is like being able to find all of the arrays representing phone numbers or meaningful words, amongst all possible sequences, merely based on the properties of them being arrays.
We transfer paradigms from following procedures to properties.
Likewise, each programming language has its use cases. A node-based visual programming language, offering a noodling workflow, is easier to use for the design of video game textures than manually coding the image, weighed down by entering letters and semicolons. Most likely, it has fewer bugs, too.
But transferring the visual and the written languages into the realm of mathematical foundations allows us to describe a specific correspondence between them, something that doesn’t exist as part of the languages by themselves.
Because mathematical practice is mystified, and we believe its bond to software is merely referential, many obstacles lay on the road to the symbiosis between mathematical foundations, computer science, and “real-world” programming.
When independent communities at the heart of software innovation get stuck in the same cognitive traps repeatedly, the crooked struts of the microcosm ripple through the wider corporate organism.
Since the scientific work relevant to trailblazing hobbyists’ creative experiments is unknown, and the industry winds are yet to be intertwined with academia, both need to start speaking one another’s language — beginning with understanding the essence of mathematics and intuition behind abstract mathematics, such as category theory.
Without the intuition, theoretical ideas from mathematics are treated as universal stencils, verging on the boiling point of redundancy.
Abstractions are only helpful if they’re meaningfully chosen. Intuition based on mathematical foundations prepares our cognitive models for selecting fitting abstractions, parting from the abuse of jargon and complexity.
Thank you for reading! In the next chapters…
The logical tapestry of mathematics through the lens of an alternative number theory
The algebraic and graphical structure of software
Want to find out more about Practical Paracosms?
References and credits
Cover image by DeepMind
Special thanks to friends Daan and Prathyush for the constructive criticism on my drafts.
“Digitising mathematics” is very much the courtesy of the amazing Xena project.



So cool! I would really love to read more about your work on Idu and the process of exploring mathematical formalisms for procedural generation :)